Published : May 23, 2023

Part of a series on Line Rendering!
Published : May 23, 2023

Part of a series on Line Rendering!

Soooo! As you may or may not know, I've spent the better part of last year working on lines. While I still have much more to find out, I think this is a good moment to reflect back at what I've learned!
This series of articles will an overview of the whole subject of line rendering, filtered through my own understanding of the domain, and coloured by my experience as a 3D programmer for video games. We'll look at the theory and the detection methods in this first part, then how to stylize lines in part 2, and finally how to put that into practice in part 3! I'm not going to cover every detail, but it should give you a fine map of the field.
Since this subject is kind of halfway between art and tech (and quite complex from both), I'll assume people can come from either. To avoid making this article heavier than it already is, I've added :messages that you can show by clicking on links like this. They'll hold some additional detail or explanations for the concepts we are going to cover!
In this first part, we'll look at some theory behind lines, and then see some of the methods we can use to detect them, so let's get started!
Yes, just like that! Bonus reading material for you.
Honestly, this subject is very technical and I won't be shying away from it, so take your time, maybe reread some parts later, and don't hesitate to pop on Discord to ask questions!
You already know what a line is, but when we dive deep into something, we often need to redefine elements in detail. I'll cut to the chase by enumerating some properties:
Now, our issue in rendering lines is not just to draw them on the screen (which is in and of itself trickier than it seems!), but to also find where to draw them. And since this is stylized rendering, they don't always follow a strict logic! So how can we go about this?
Well, turns out in 2008, :Cole et al asked that same question: Where do people draw lines? The answer they found is that it tends to be very related to the object's underlying geometry, as people tend to draw the same lines at the same places. The most important ones are what we call occlusion lines, when one object is in front of another. There are most often found where a geometric property changes sharply, like a bend for instance.
I think this is linked to how we humans process visual information, as our brain will try to separate objects and simplify shapes by finding boundaries. The reason why line drawings may be easier to look at is probably due to to them having already done that work for us.
The nice takeaway of that, is that we will be able to find most lines by analyzing the underlying scene!
So we know that lines are linked to geometry, but how exactly? This is why it is useful to classify them, as not all lines will be detected in the same way. I'm evaluating lines based on those 4 categories, plus a bonus one:

(Please note that this is a simplification that I found useful, because if you look closer you get more questions and it hurts my brain.)
As we have seen, these are located where a geometric property changes. How a property varies over a surface is called the gradient, and I'll be using that term for the rest of the article. These can be the depth gradient over the image, or the surface gradient, or the light gradient. They can be computed mathematically, and we use that to find some interesting properties, like where the gradient is very high.
On top of that, we have what we may call the order of the lines, related to how much the underlying geometry has been derived. What this means, is that to find first-order lines, we look at variations in the surface, for second-order lines, variations in the variations of the surface, and so on. Higher-order lines tend to be more complex and more expensive to compute, so we'll just look at first-order lines, but you may read the work of :Vergne et al (2011) if you wish to know more.
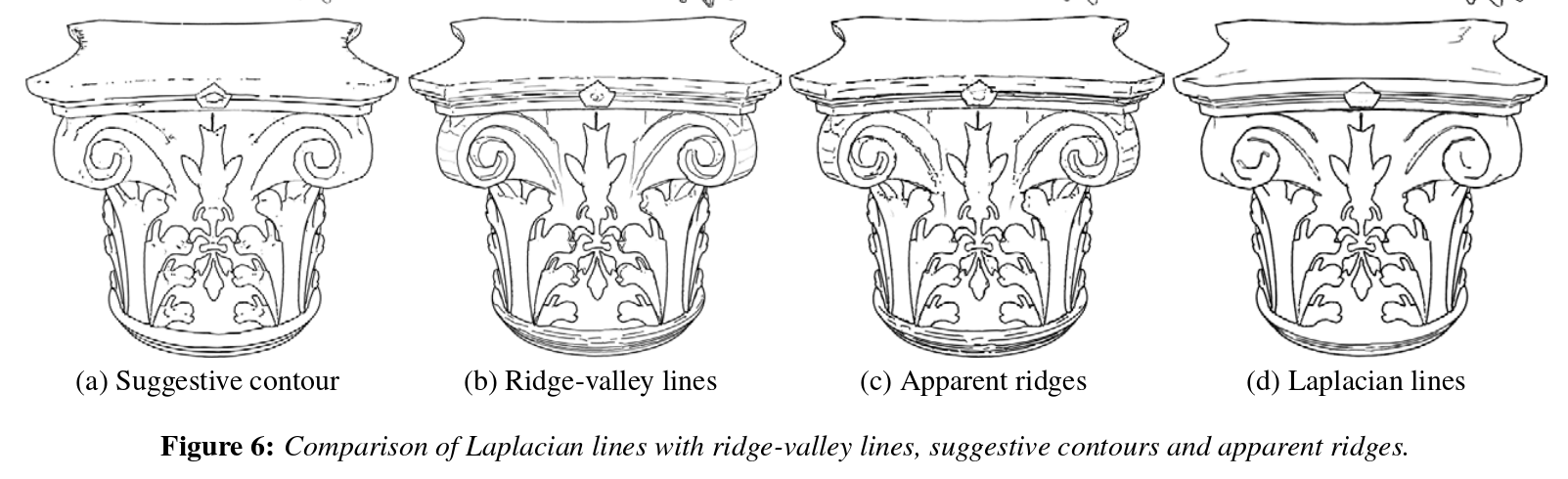
The subject is vast enough as is, so there are some line types we won't really cover how to detect in this part, but you may still apply the same stylization techniques on them by treating them as arbitrary lines. These include:
Since lines are dependent on geometry, we can find where they should appear. Different types of lines may be found using different algorithms, and the algorithm choice will also affect how you may style and control that line. Tricky!
Most algorithms may be found in one of two categories, the screen-space ones, and the geometry-based ones. But before that, let's take a look at some rendering tricks that have been used over the years.
The title is a bit provocateur, but you know we love ourselves some quick and easy wins. These methods have been some of the most used, and are usually born of limitations in the graphics pipelines, sometimes from even before we had shaders. We got a lot more flexibility today, so it's a bit unfortunate that this is still the state of the art for many games.
Instead of trying to find the edges proper, these methods rely on particularities of the graphics pipeline to "cheat" and approximate the solution quickly or in a simpler way. As such, they can work in the specific context they were made from, but may quickly fall apart in other contexts.
While it is possible to expand upon them, I think you would be better served in those cases by implementing a more proper method directly. These methods shine when you want a quick and easy result, but may lead to very complex setups when trying to compensate for their weaknesses.
The poster child of this category, and absolute classic of the genre is the Inverted Hull. By creating a copy of the model, extruding it a bit, and rendering the backfaces, we can make a sort of shell around our model. This does reproduce the Occlusion Contours pretty neatly, which is why it has been used in a lot of titles like Jet Set Radio.

This method however presents a lot of limits. The processing cost is somewhat high, considering we are effectively rendering the model twice. It is also very sensible to artifacts, as geometry may clip through the line.
One thing this method is good at however, is that you can get some nice control over the colour and width of the line. The latter can be achieved in several ways, the most efficient of which is by adjusting the width by vertex using a geometry shader. This is the method games like :Guilty Gear use, and is a very good way to control this intuitively and avoid some of the artifacts. However, this adds another necessity: the normals of the model must be continuous, otherwise you may get holes inside your hull.

Overall, this is a nice method and a smart trick. It has some good basic control on the line's visual aspect, and is simple to put in place, which can make it pretty useful even with its flaws. However, there is one final flaw which I haven't directly brought up: :this method ONLY finds Occlusion Contours. This means that, to find the other line types, you must use other methods.

An example image showing common artifacts of inverted hull: sharp edges splitting, lines disappearing because of clipping. We'll see how to handle those in part 3. The game itself is an indie fighting game, FrostFire, that you should definitely check out!
As a side note, you can also hack together some janky :contour lines quickly using the Fresnel factor.
Another method for contour lines is Fresnel / Rim Lines. This uses the fact that the Fresnel factor is related to how "side-on" you're seeing a surface, which is correlated to the fact that most contour lines are gonna be around "side-on" surfaces, to draw some part of the model in black.
The main flaw here is that word: "most". This is very affected by the geometry, meaning that you may either get a huge line, or no line at all, depending on the object. I don't recommend using it, but I find it interesting to mention.

That's not entirely true, as you can still use a similar method to get the sharp edges for instance, which is what :Honkai Impact did. This however requires an actual preprocess step not far from the geometrically-based lines we will see later, which means it will only find the edges that are sharp at preprocess time, and won't update with the object's deformations. This means that the method works best for rigid transformations (only affected by one bone), like objects, and not so well for organic parts.
However, if you are making a preprocess part in your pipeline to get those edges, you are losing a lot of why you may use the inverted hull in the first place, which is the technical and time barrier. By implementing this, you pretty much prove that you have both, and could have used that to implement another method that may have suited your case better.
For Mihoyo's use case, considering they DO use another method for their environments, I believe they did this for a few reasons:
If you are in a similar situation, you'll probably be better served by a screen-space extraction method, which we will see below!
The other types of lines being independent of the point of view, they tend to be prebaked onto the model. Yes, this is effectively Arbitrary Lines methods, used to approximate some other types.
Intuition would tell you to just draw on the model, and be done with it. This works, but the line may present a lot of artifacts and appear aliased. This is why you can find two methods to do that.
One of them has become popular because of its use in Guilty Gear, owing to the fact that it's one of the first commercial projects to have nailed the anime artstyle and being one of the few known complete workflows. I am talking about the Motomura Line, which has been brought by Junya C. Motomura.
The concept is simple: you still draw the line as with the previous method, but you align your texels with the geometry (id est, you make it horizontal or vertical). This alignment will prevent aliased texels from changing your line.
The main issue of the method, is that it is very manual, and adds a lot of pressure on the topology to make it happen. This is not ideal, as topology is already under a lot of constraints, especially for stylized rendering, and having one find a middle ground between shape, deform, shading, and lines, is going to make it harder.
You may see some people use Square Mapping to refer to that. I don't really like to use that name for the method, because it sounds more generic, and that concept may be used for things outside of lines. I also don't think it should get a separate name, because it is just an extension of UV mapping, but hey that might be just me.
Another method is to just do it geometrically, just put some quad or cylinder to make that line. It works, but it either makes the line's width vary with the viewing angle (quad) or extrudes the line a lot (cylinder). This also opens up clipping issues.
But, by using one of those two methods, you may thus have a more complete render! This is how a lot of higher end stylized rendering productions are made currently.
All the methods we described earlier have been artist-developed, and came a lot later in the history of rendering. But, even before that, some cool early programmers also looked for ways of rendering lines, with even more restrictions, but also a direct access and understanding of the pipeline.
Nowadays, these methods are not as useful since we know how to do better, but I think it is interesting to show them, especially as you won't really see them mentioned outside of really specific contexts.
One of them is called the Hidden Contour by :Rossignac and van Emmerik in 1992, and is kinda analogous to the inverted hull. Here is the trick however: here we don't add an additional mesh, we will change the rendering parameters to draw the same one again! Here are the changes:
I find pretty interesting to see how the same concept as inverted hull gets implemented when going at it from a programming side, but this also means we got the same need to render the other edges. However, this is programmers we're talking about, before we even really had DCCs, which means they tend to look at more automated solutions.
This is where what I'll call the Hidden Fin by :Raskar in 2001 comes in, which can detect sharp edges. You create, under each edge, two small quads. They share their common edge with the edge they are testing. Their dihedral angle is set at the threshold the user sets, and is independent of the geometry itself.
What this means, is that if the geometry is flatter than the hidden edge, it will stay hidden beneath the surface. However, if the geometry is sharper, the edge's quad will show though the mesh, displaying the line!
This is a geometric way to represent that test, which is find super cool! It's not really the most practical in terms of rendering, because it does require a LOT of geometry, but it's a nice concept.
Nowadays, the additional control we have allows us to have more robust drawings, and better optimizations, but this is pretty smart and interesting to see!
So why did I mention all of these methods, if better ones exist? There are several reasons, one of them being that I think it's cool, but it was also to address their use.
These tend to be the most known methods, and are mentioned in a lot of places, but with not a lot of context. Now that you have a better framework to see the limits, you should be able to know when to use them effectively.
The main risk with hacks, is when you try to extend them beyond their field of application. They can be pretty fickle, and you may very well be over-engineering solutions to problems that already have some. This will consume a lot of time, and may lead you to worse results than if you used another of the methods I will present here.
Another reason why I showed them, is that the method may be used elsewhere with good results. For instance, the inverted hull can be used to make some nice looking two-color beams! Another use is to make some parts, like eyes, easier to make, but then that becomes a hack for shading (which I might address in a future article, but hey one at a time).
However, an unfortunate fact at the time of writing, is that getting access to the other methods may be sadly beyond the reach of most people. Indeed, the other ones require nodal or shader programming, and can really depend on the final graphics engine. A lot of the currently available engines don't really open up their graphics internal, because it's a very complex subject, but here we kind of need it.
While the algorithm may be easy-ish, integrating it into an engine can be very tricky. I really can't fault people for not shouldering the cost of implementing these methods and just using a hack. I can certainly hope it becomes less and less as time goes on, so that we can get cooler renders!

My own game, Kronian Titans uses more advanced SSE methods to give the lines more texture. I'm still not done iterating, but I like how it looks!
Next up is the current standard method: screen-space extraction (SSE). This family of methods boasts the quickest basic speed of all, while being able to detect a lot more line types, but are trickier to control and have some trouble with the control of the width. They are also a bit more complex, which can make them quite limited or tricky to implement without opening up the graphics engine.
The method is based on an algorithm known as convolution: for each pixel, you do a weighted sum of the surrounding pixels, and output the result. Which surrounding pixels and their weight is known as the kernel. This might be a bit tricky to understand if you don't already know it, so you can :expand this to get a quick explanation! Convolutions are pretty good at edge detection if using the right kernels, and even a simple Laplacian can get us pretty far.
The key to understanding this method however, is to realize that we don't do our convolution on the regular output, but on the internal buffers, sometimes even custom made for this pass! This is what allows us to get good precision and better results than, say, a :filter. We can thus make several convolutions on various buffers and combine them to get advanced results:
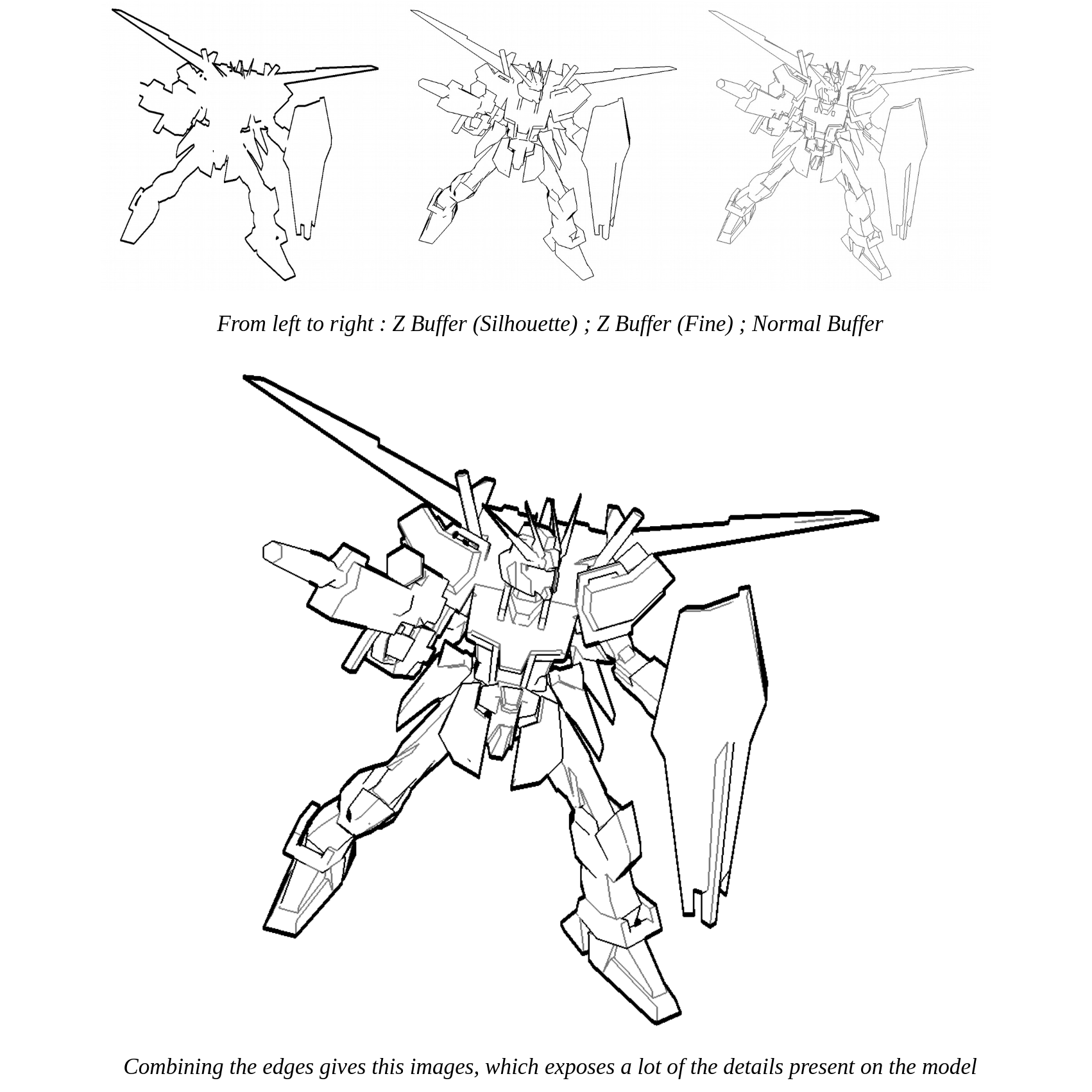
The fact that it's screenspace also helps the lines feel coherent at any scale, which you would need to compensate for with the previous hacky methods. Overall, this is a really good method that can also scale with your added demand for control and style, although each step makes the solution more complex. If you get out of this article remembering only one method, this is the one you'll want to use in most cases.
Let's now take a deeper dive into the subtleties and various aspects of the method.
A filter in this context is an image processing algorithm that runs on the rendered image, not internal buffers. The advantage is that they may be applied to images from any source. The disadvantage is that they have more trouble finding the parameters from the final image itself.
They tend to be a lot more involved and expensive, but also tend to provide a lot less control, working more like a black box that will output the stylized image. This is the main reason why I think they are ill-suited for games. They also tend to not really keep a coherent stylization from one frame to the next, although that depends on the algorithm.
Similarly, you may have seen a lot of machine learning methods floating around, and while there are many ways to apply it to rendering, you might be thinking of those automatic stylization ones or style-transfer using GANs. While cool, they tend to present the same problems of regular filters, but turned up to 11, so I wouldn't recommend that direction either.
Blurring is a somewhat simple operation to understand: you want to average the neighboring pixels. A naive algorithm will probably have a loop accessing all relevant pixels, like this:
def BlurPixel(img, x, y, blurSize=1):
blurredColor = Color()
for j in range(-blurSize, blurSize+1):
for i in range(-blurSize, blurSize+1):
blurredColor += img.GetPixel(x+i, y+j)
blurredColor /= pow(blurSize*2+1, 2)
return blurredColorThis is functionally identical to what a convolution would do, with a 3x3 kernel, where every value is 1/9, as you can see on this schema:
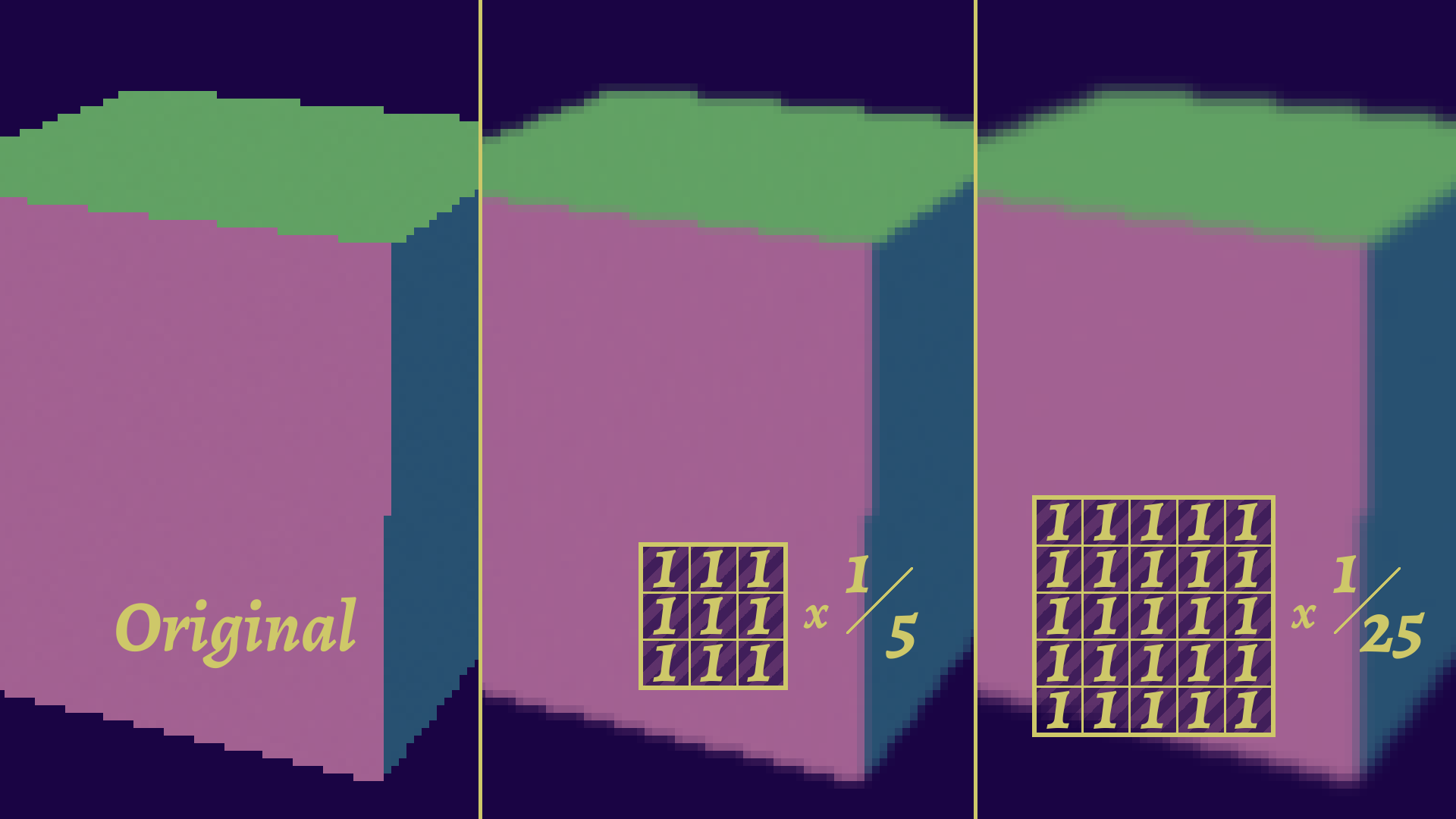
There are a lot of applications (like neural networks) and subtleties to convolutions, as they are also good at edge detection. Doesn't that sound useful for our use case ?
A convolution is basically a mathematic way of comparing neighboring pixels. You have a small pattern called the kernel, centered on the pixel you want to compute, where each pixel has a defined weight. You then use those weights and pixel values for a weighted sum, and then use the result as you wish!
Let's use an example with a Laplacian Kernel, which is a simple way to find the differences between neighboring pixels:

This is equivalent to taking the center pixel, multiplying it by -4, and then adding the 4 directly neighboring pixels (up, left, down, right). What the formula does, is basically compare the center pixel to the average of its neighbors: if it is close to zero, it means they are nearly identical.
We can use that together with a threshold to find discontinuities, areas where the value changes quickly, which is exactly what we need to detect edges as we will see in a bit! If you want a second example about convolutions in general, you can :expand this section.
I touched a bit quickly upon that, but convolution is only one part of the answer, the other being the internal buffers we use. The answer will depend once again on the type of line we want to find, so let's take a look through them once again.

So that's our easy lines out of the way. Let's continue with some trickier ones.
The method can detect most types of lines, especially mesh intersection (through object ID buffers) and shadow lines, which are very tricky geometrically. It might however have some difficulties with higher order lines (which would be expensive to compute).
This may be pushed further through the use of custom buffers and shaders, depending on the type of data you are manipulating. This can either be used to optimize your detection, by packing all the needed values inside of one buffer, or by outputting specialized values (like the shadowing mask). This is in fact what Kronian Titans does, by combining its three ID-based detections into a single buffer.
In this part of the article, as I am still only talking about extraction, I am styling all the contours the same for simplicity. Know however, that as you find each contour separately, you can also flag them separately, and thus style them separately. You just have to include that functionality when implementing your shaders.
Now, that's the base idea, but we might still get a few artifacts. This section is about how to improve our results a bit. This is not always applicable to all line types.
The first order of business is going to be improving the threshold, which is very useful for contour lines. Indeed, since we're using a flat threshold, we are just looking for an absolute difference in distance from the camera. This usually works, but can break down at glancing angles, and you may find false positives. However, increasing the threshold wouldn't work either, because it might miss objects that are close together.
Here, it's easier to see in an image:
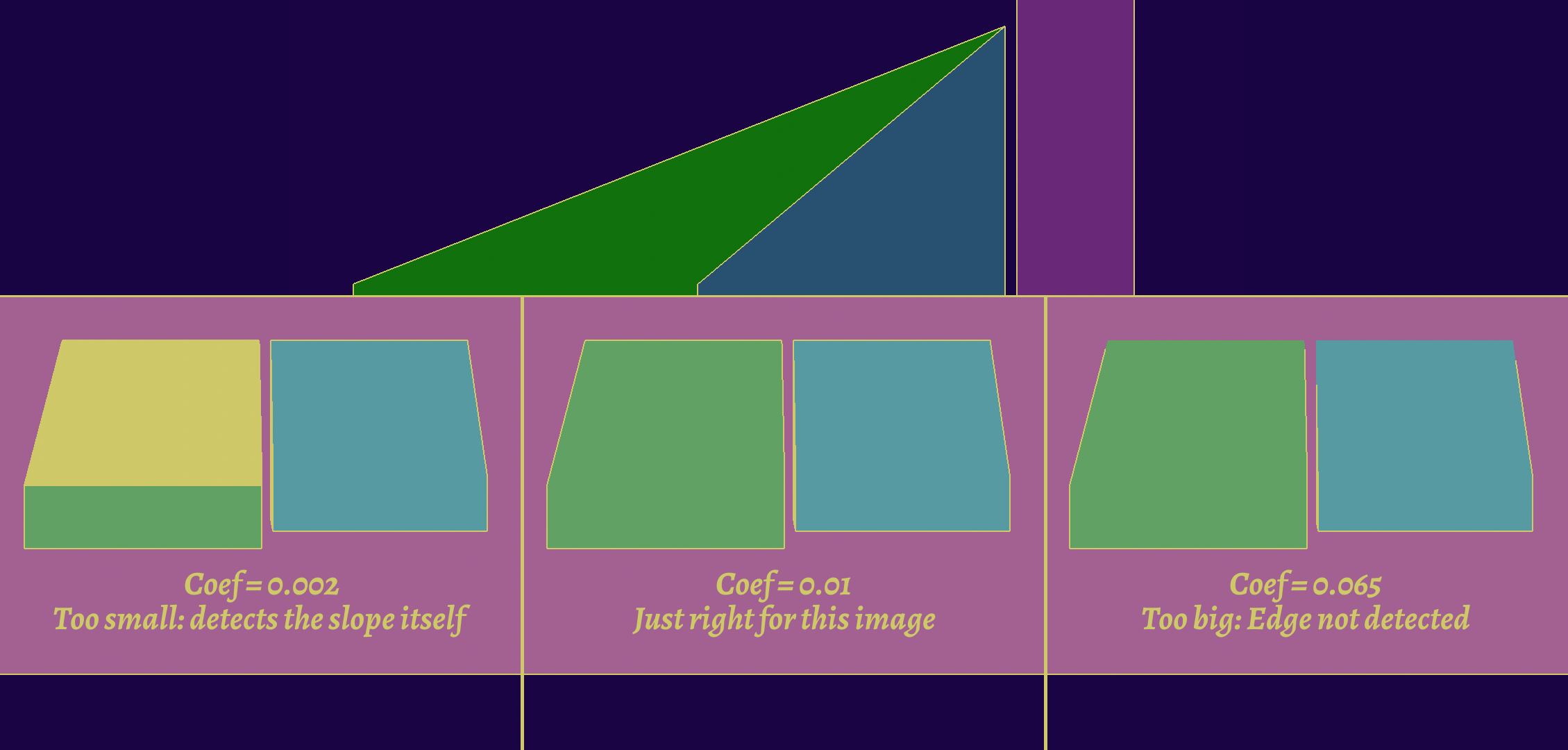
One solution would be to adjust the threshold depending on the slope of the surface, which we can know by taking the normal at the central pixel. The exact formula depends on implementation.
Unfortunately, this adjustment might make us miss lines we would otherwise find. It's a fundamental limitation of screen-space extraction algorithms, as we may only rely on information we have on screen. The main way to improve this would be to use :several detection methods at the same time, but this might bring some limitations in the stylization part.
As it can be common, sometimes the best solution isn't an algorithm that can handle everything, but a combination of specialized algorithms.
In this case here, adding more detection will reduce the conditions for this to happen. So for instance, detecting normal discontinuities will find the previous example, but not faces that are parallel. Another way would be to use object IDs, meaning as long as it's two different objects, it will be detected.
This is not to say that they don't have failure cases, but by combining them the remaining failure case is really hard to come by: you need that the two faces are parallel AND very close AND part of the same object for the line to not be detected, meaning the artifacts are going to be very few.

Another way to improve detection is to use different kernels. Right now, we've been using a simple Laplacian kernel.
The classic has been to use Sobel kernels for edge detection. It's actually two kernels, one vertical and one horizontal, that you combine the results of. Compared to Laplacians, this catches some edges better on the diagonals, but also slightly more expensive, as it requires 9 texture accesses compared to the 5 of a simple Laplacian Kernel. The dual kernel nature also means you can use only one of the two directions to only get vertical or horizontal edges for instance.
An addition to that has been Scharr kernels, which are optimized Sobel kernels that handle diagonals better and are tailored to the hardware limits. For instance, where a regular Sobel kernel will use the coefficients 1, 2, and 1, the Scharr kernel for 8 bit integers (incidentally, a color channel in most images) are 47, 162, and 47.
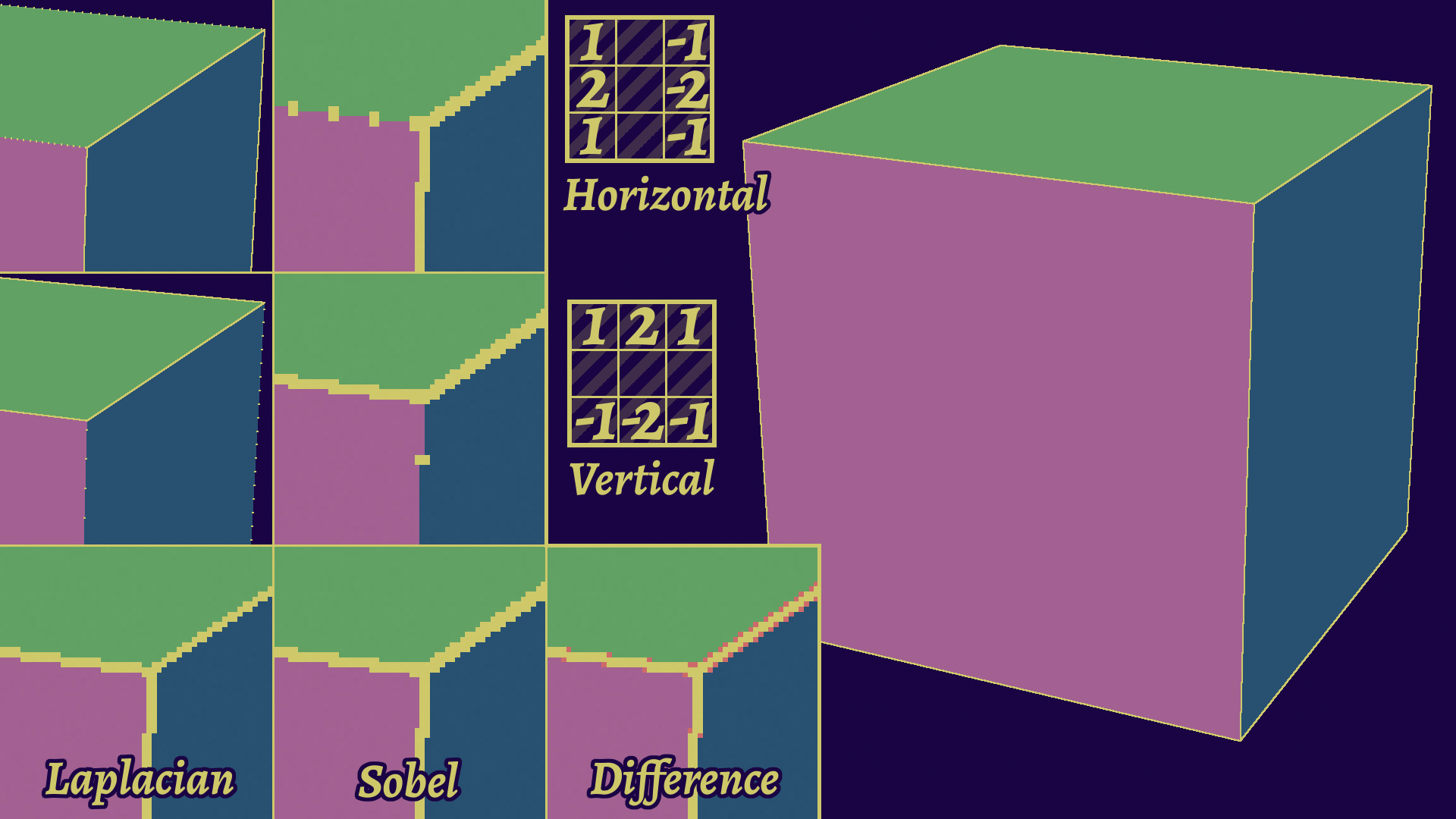
There are, of course, other edge detection methods, which are outside the scope of this article. Some examples include the Canny edge detector, or the Difference of Gaussians operator. They tend to deliver better results for photographs, but can be a bit (or very) slow, and trickier to pass parameters with, so I prefer sticking to the simpler ones.
Something to also note here is that I've only presented 3x3 kernels, which is in my opinion sufficient. But, if you want to go for bigger kernels, like I don't suggest you do in the next part, you can find more suitable coefficients online.
At this point, we have a way to detect lines, but the issue is that our lines are all the same size of one or two pixels (depending on if you're using absolute value or not). This is problematic because it limits the amount of styles we can express and our ability to remove specific ones. This is actually two problems, one of them is actual control which we will see in the next section, and the other is enabling it, which can be tricky in screen-space extraction.
We can now detect lines, however an issue remains in that our lines are all the same size of one or two pixels! This is problematic, because it limits the amount of styles we can express and our ability to control it. In order to unlock that, we will have to start by being able to have thicker lines.
One might get the idea to start using bigger kernels to detect lines from further away. This actually works, and you have two ways to do it, but each have flaws.
There are a few additional tricks to these methods including rotating the kernels, but bigger kernels naturally tend to have some noise in line detection, as you may detect features that aren't local to your part, which might translate into artifacts.
In order to avoid these problems, we can use dilatation algorithms, which expand a line using a kernel. The basic idea is just that, they'll check the whole kernel and if they find any pixel of the line, they'll expand.
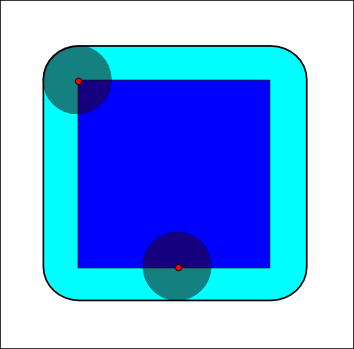
"The dilation of a dark-blue square by a disk, resulting in the light-blue square with rounded corners." - Wikipedia
This is naturally a lot more precise, as you keep the detection local and then make those lines bigger, but a naive implementation will be just as long as a bigger kernel. Therefore, we will prefer using several dilatations one after the other, which can be often implemented using ping-pong buffers.
While you could start thinking about what is the most optimal number of passes and kernel size for a given width, I'll cut to the chase, since we can solve that problem with the Jump Flood Algorithm. The basic idea here is to sample from further away at first, and then halve the distance each time. This allows us to dilate more with each step, making the algorithm log2(n), which in layman's terms means "very very fast". If you want to know more about the implementation of such an algorithm, this article by Ben Golus will interest you.
At this point however, you might have noticed that we still widen all lines homogeneously. This isn't enough for the control we want to achieve, therefore we will need to compute what's called the SDF (Signed Distance Field). To simplify, this is about computing the distance to our line instead of a flat "our line is here", which then means we can adjust it or do cool effects.

Thankfully, computing the SDF is very easy with line dilatation methods, so we don't have to change anything really for those. :The methods using the kernel technically can, but it's kinda hacky.
There is a small point remaining, which is about if the base line is one or two pixels wide, but this will be explained better in the next section.
To illustrate, this is what I'm using in Kronian Titans. It IS slower and less precise, but it allows computing the SDF in a single pass, which is pretty useful in Godot 3's limited renderer.
The idea here is somewhat simple: you sample in a pattern, but associate each sample with a distance. Then, you take the minimum distance of all the samples that detect a line.
This method is very affected by the pattern choice, as more samples is more expensive, while less samples will introduce bias and provide less precision. Ideally, you want a rotationally robust kernel, or even rotate it to limit that bias. I would also force the closest neighbors of the pixel to be checked each time, to ensure you don't miss lines. Kronian Titans uses a variation of the 8 rooks pattern I did manually.

Kinda spoiling the article hehe, but yeah I believe that at the moment, Screen-Space Extraction algorithms are the best choice for games. For offline rendering, it's a bit debatable with the next method.
In my opinion, it's a bit hard to argue against, really:
Hacks' only advantage here is that they are easier to implement, which may be unfortunately a breaking factor for your team, and that's okay. It's a bit unreasonable to ask to open up the renderer and code a ping-pong dilatation algorithm inside a complex game engine, so I hope this becomes easier as time goes on. We will see how to implement all that in part 3.
SSE algorithms have however one fatal flaw: stylization can be pretty hard or limited! This is especially true for a simple common case, which is pretty hard with SSE: lines that change width as they go on! This is where the next family can help us.
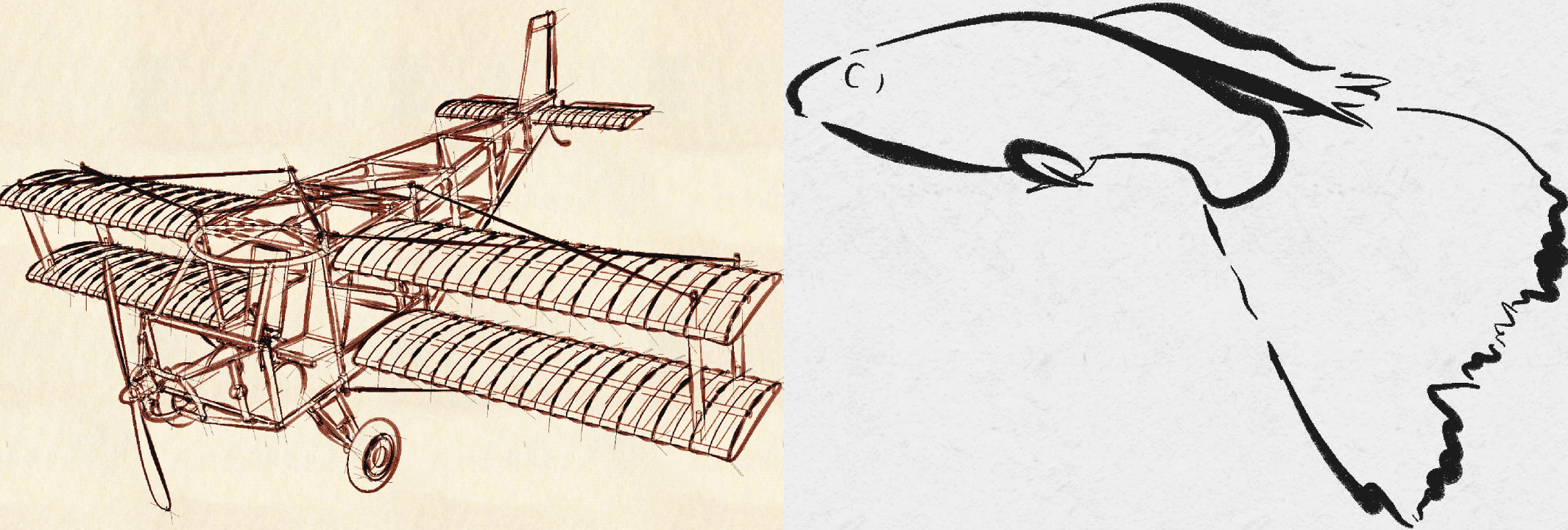
3D renders from :Grabli et al's 2010 paper, using different styles. This method allows us a lot more freedom in rendering!
And finally, the last method: mesh contours! These work by analyzing the surface itself, edge by edge, and extracting lines that way. I have no video game example, but you might have seen them in Blender Freestyle.
The biggest difference with other algorithms is that you have line primitives, as opposed to independent pixels. This unlocks a wealth of additional options, like varying the width, combining or simplifying lines, drawing them with textures like dashed lines... There's a lot!
The line types that may be found are the same as SSE methods, with two exceptions: geometric methods can find :hidden lines behind the model, while SSE may find :model intersection lines a lot more easily.
There's however one main issue: this is slow! Often not even fit for real time! The previews being slow also doesn't help working with them. Additional problems include the complex algorithm implementations, and the complex control available. You absolutely need control over the rendering pipeline in order to deploy this.
In fact, this article has been cooking for so long that I can now say that I'm working on that problem, as I have released a poster as part of my PhD work!

There's a very good state of the art by :Bénard and Hertzmann in 2019 on this whole subject if you wanna learn more! And I'm not just saying that because Pierre is my PhD advisor and read this article.
So, it's not exactly true but close enough. Geometric methods will find hidden lines by default, with steps needing to be taken to hide them, and SSE will only extract what's visible in the buffer.
In the buffer being the keyword here. By default, SSE methods will only find visible geometry, but if you don't render geometry to a specific buffer, it won't be taken into account. We can use that fact to create additional buffers with the objects we want to see even when hidden, which is a common effect in games for seeing characters through walls. This is usually done by having a second depth buffer and comparing the two.
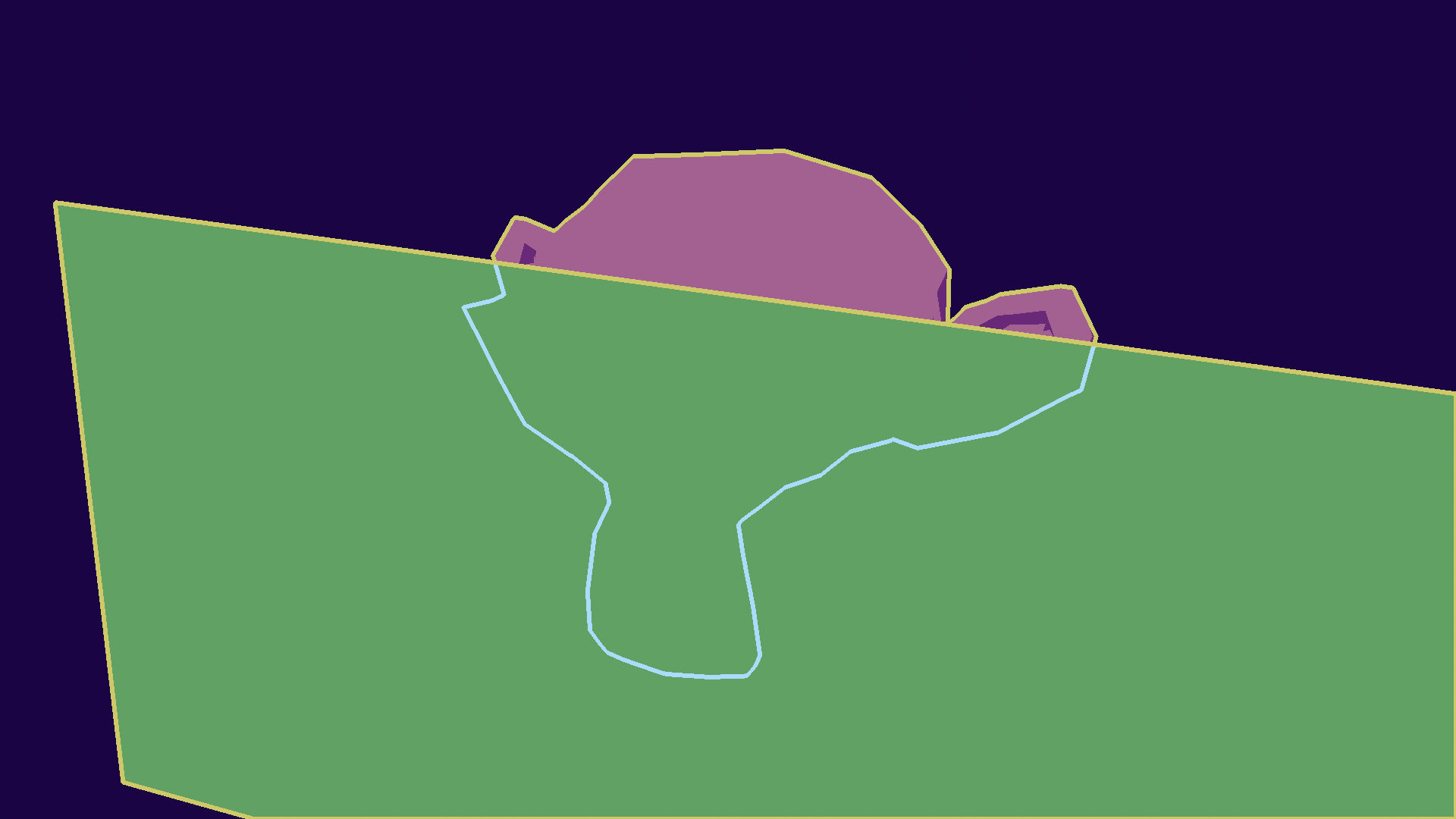
Again, not exactly true but you'll suffer if you try to implement it. Geometric algorithms don't care about intersections at this step, only focusing on their own little part at a time. Finding these lines will require you to take the whole model into account to find self-intersections, and the whole scene for general intersections. This is also another family of algorithms, collision detection.
Compare this to SSE algorithms, where it's just comparing two pixels on an object ID buffer to find inter-model collisions. Self-intersection is a bit trickier, but by default you'll still find discontinuities, and between material IDs and sharp edges you'll very probably have a line at that intersection.

My current line of work is trying to find a way to use them in real-time in video games! Video game rendering has a few strong constraints:
Most optimizations we know of also only target static meshes, meaning they may be used for environments only. This is an issue, because the usual target of line rendering are characters, which have varying geometry but fixed topology.
All of that together makes it so we don't really know a way at the moment to have mesh contours in our games, but there are some really interesting steps towards that, with for instance :Jiang et al (2022) which released this summer and managed to have mesh contours in about 2ms in Unity, albeit with some limitations. It's main additions are in the line processing steps of the pipeline, so we'll talk about it in part 2.
In any case, this is what I am currently focusing on, so uh stay tuned? We'll see how it goes.
General extraction of lines tend to be pretty straightforward in most cases, as you'll use the same geometric properties. Here's how it goes:
Efficient extraction will need to create buffers. The simplest way is to use a Winged-Edge structure, meaning that each edge will have information on its two endpoints, but also two neighboring faces. The most efficient way is probably to keep only IDs to each of those, as they will be referenced by multiple edges.
Then, the algorithm is just iterating over the edges and computing what you need, and then registering the edges that satisfy those constraints. This algorithm is a lot more efficient on the GPU, especially if you manage to keep occupancy low, as it's simple computations.
Contour extraction is going to be the complex part, as depth discontinuities are not local. We can thankfully use other geometric properties, by defining a contour edge as a point where the normal and view direction are perpendicular. We can express it in simpler terms however: if one face faces the camera, and the other faces away from it, it's a contour edge.
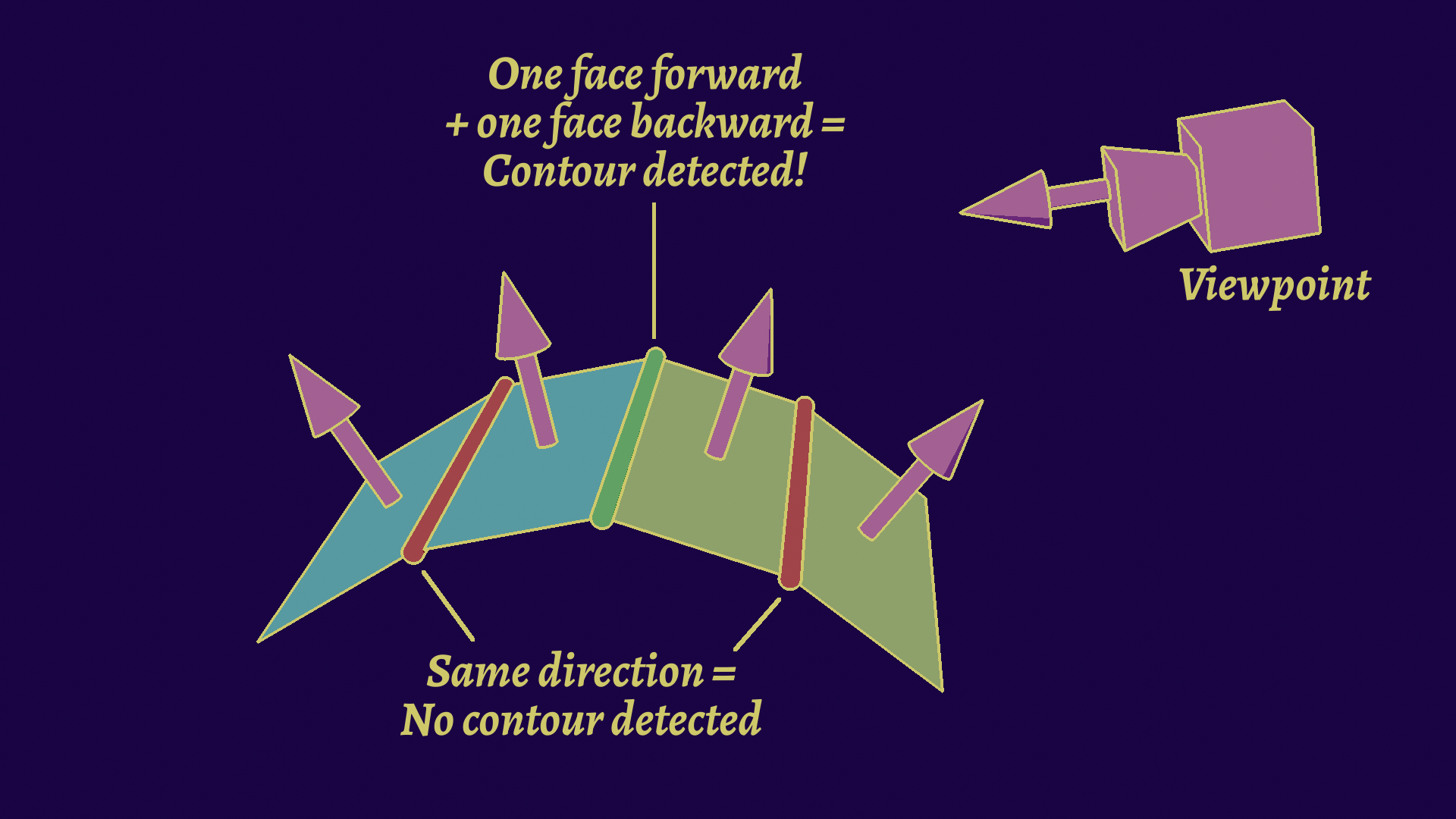
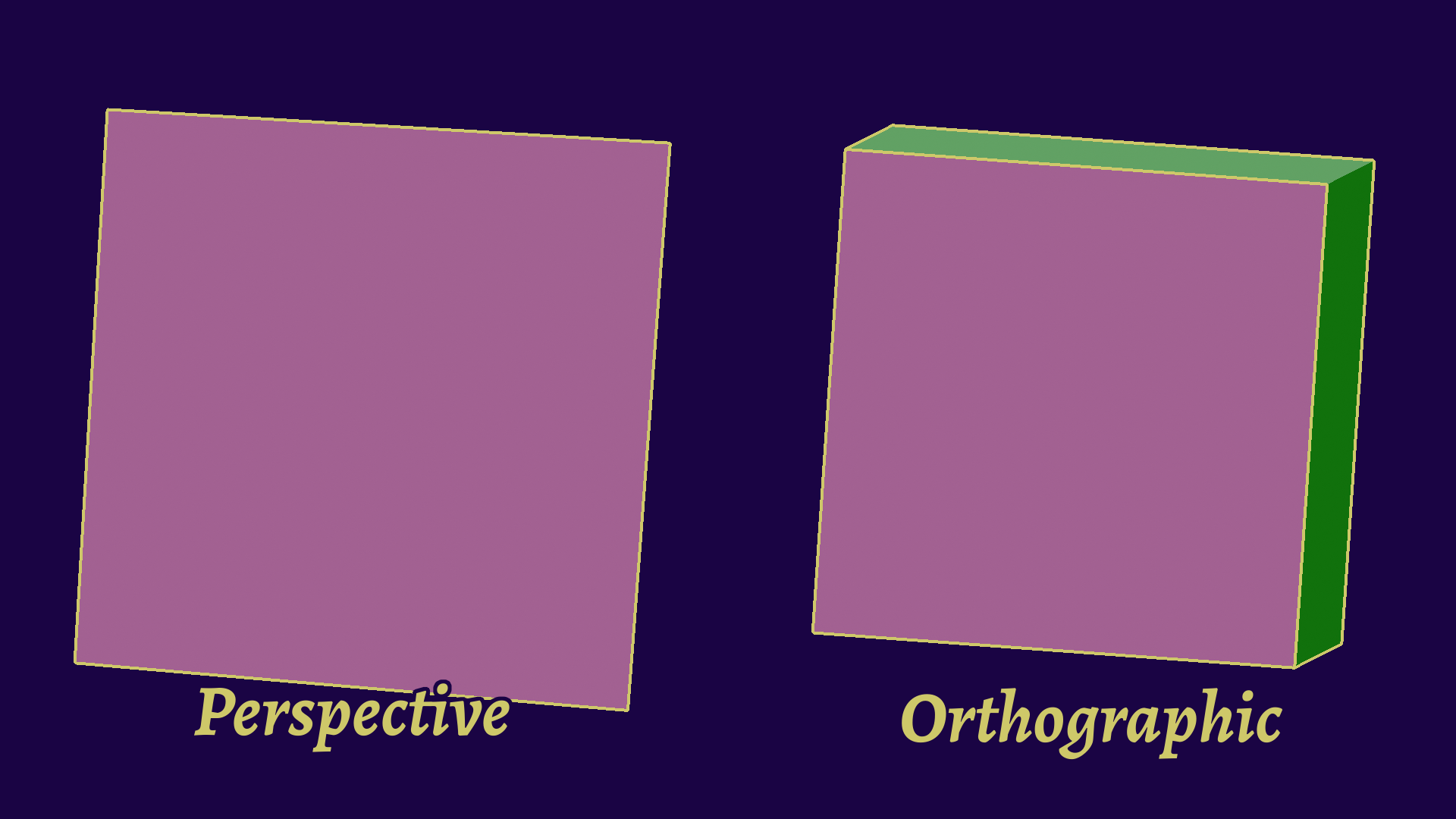
An additional step you need to make is to recompute the view vector from any point on the edge and the camera's position. This is only needed for perspective projection, as the deformation will alter the exact contour edge for the picture. While this seems small, it actually complexifies a lot of the optimizations later on.
An alternative algorithm to testing edges is testing faces, by using the geometric normals at each vertex and then using linear interpolation to find the accurate edge. This is an extension of using triangular meshes as an approximation of a smooth surface.
Note that I wrote "geometric normal", not "shading normal". This specific algorithm doesn't take normal maps into account.
This does produce cleaner contours, as there won't be any bifurcations, but this also bring a lot of potential issues, like contours being found behind the triangular mesh. This does require a lot of additional adjustments, so for the rest of this article I'll only focus on triangular meshes.
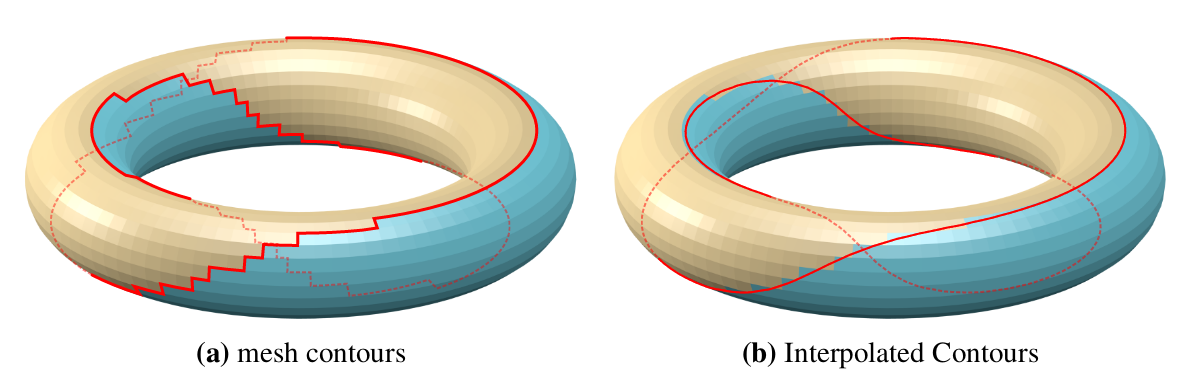
Mesh contours vs Interpolated contours. You can see the line go through the backfaces, which means it will be hidden if no precautions are taken. (Source: :Bénard & Hertzmann 2019)
In order to speed up computation, several optimizations have been found. I'll describe some of them shortly after, but first, here are some properties of contours that will help us do so:
nbFaces^0.5 to nbFaces^0.8, which means we can get very big speedups if we can guess correctly where they'll appear.Some of them rely on using the previous frames to check the most likely edges first, while others rely on static meshes. At my knowledge, no optimizations exist for characters, which are topology-fixed, and this is why it is my current PhD subject.
A few methods rely on constructing acceleration structures to make finding the edges faster, by limiting how many to check. I'll present two of them here: Cone Trees, and Dual Space. The issue with those methods is that their construction is slow and specific to a given geometry, meaning that the mesh can't change after this, limiting it to environments.
First up is Cone Trees, which has been described in :Sander et al's 2000 paper. The idea is grouping faces together into patches, in order to filter a lot of edges at once. This is done by making a cone for each patch, and checking the normal against it instead.
These cones are stored in a tree data structure, which must be constructed beforehand, as it is quite slow, but you may be able to discard more than 80% of your edges in this step!
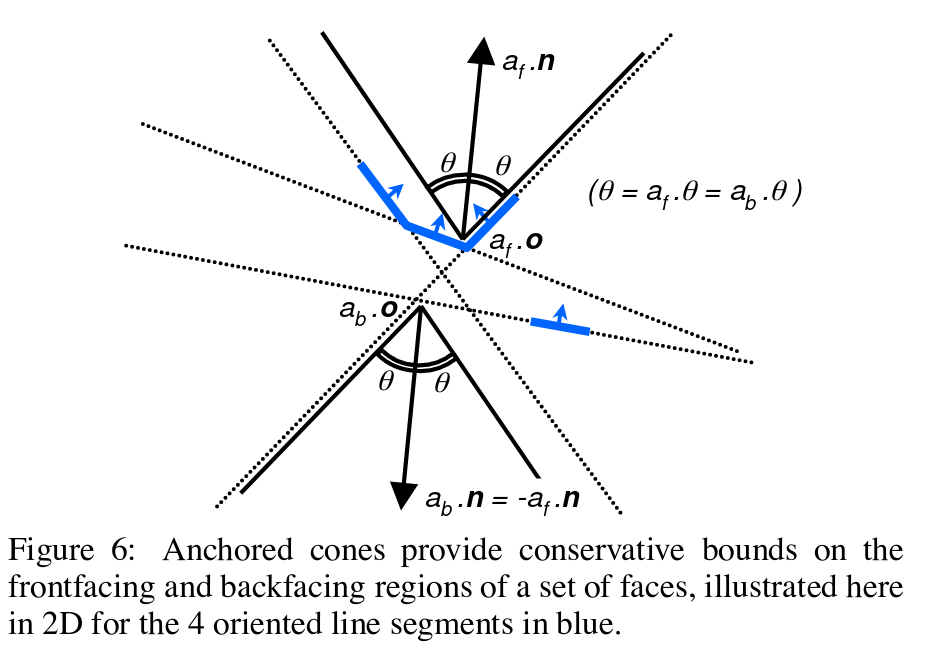
A patch along with its cone. Notice that the faces are not necessarily adjacent. (Source: :Sander et al (2022))
Next up is Dual Space and Hough Space methods. This one's a bit scarier, so I won't go into too much mathematical detail, just the basic concepts.
Let's start with the dual space transform. For graphs, like meshes, the dual graph is a graph constructed by making one vertex per face, and edges for adjacent faces. For our needs, we will also set their position to their normal, leving us with this:
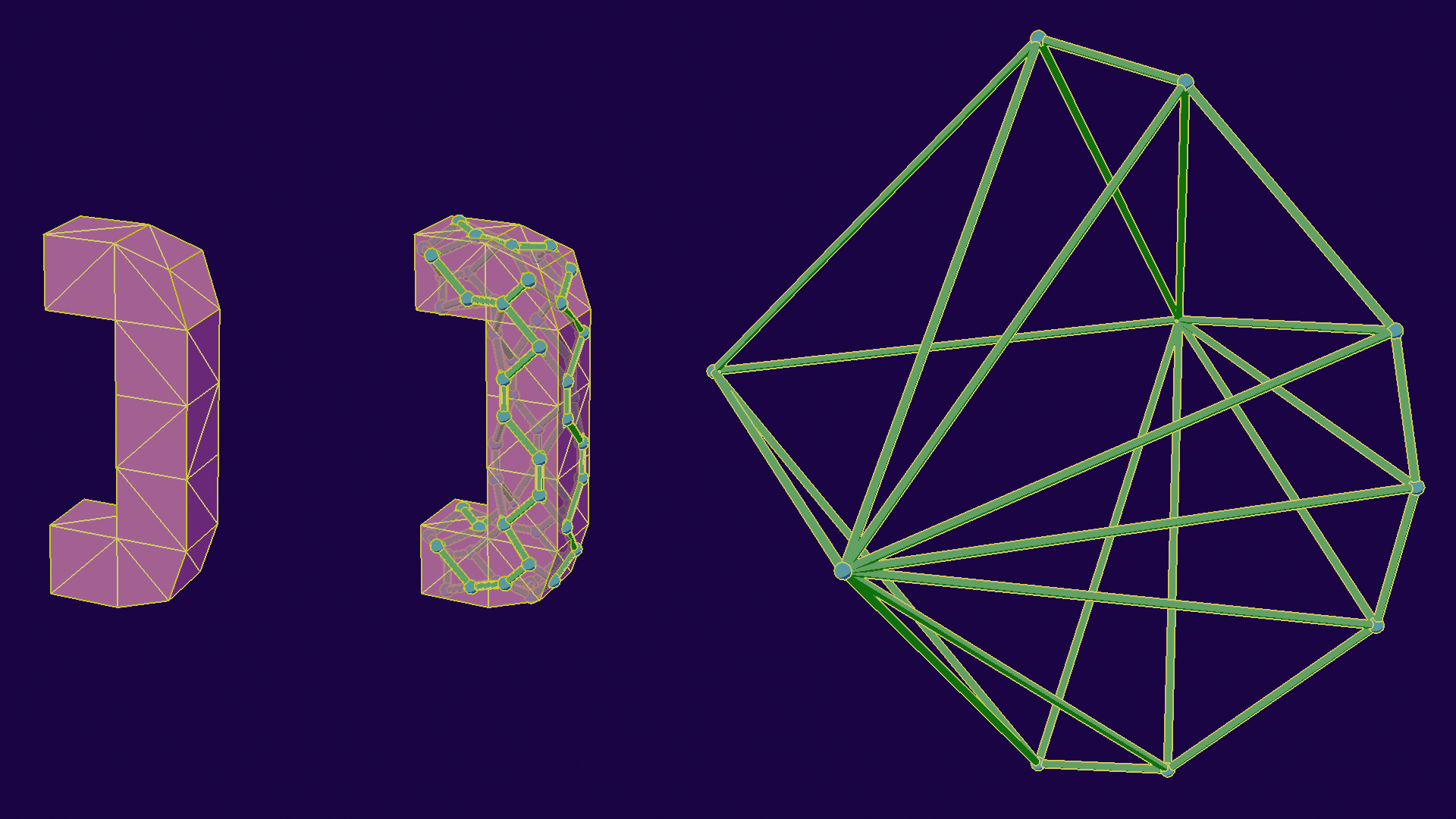
Now that we have done that, we can find contour edges by creating a plane perpendicular to the view, and looking for intersections between it and the edges. This effectively changes the class of the problem from "comparing all normals" to "look for geometric intersections", which we know to optimize better with specific data structures, like BVHs!
This is however where the perspective transform rears its head again, as the view vector will be different every time. Thus, in order to make that, you need to add an additional dimension, making it effectively 4D collisions conceptually.
In order to improve this, :Olson and Zhang have suggested in 2006 using Hough space for the computations, which has a benefit of being more uniformly spread along the BVH, speeding up traversal.
All these transformations take time, and as such must be done as a preprocess.
Please note that I am keeping a lot of this section vague, partly because it would take quite a few words to explain that in detail, but also because my understanding is still somewhat rough (I think I get the concept, but I would not be comfortable tackling 4D intersections on an hypercube yet).
When we want to make more than one image, we may take advantage of the fact that contours don't move that much when changing the point of view slightly. This means that so as long as the camera isn't making wild movements, we can use the previous frame's contours as a starting point, and explore from there.
This will raise the likelihood that we find contours quickly, and thus we may even be able to stop the algorithm early if we are running out of time with good enough results. Additional edges can be prioritized depending on their distance to a found one, since contours tend to be together, and small movements may cause slight position changes.
Similarly, we may also start our search randomly on the mesh, and prioritize edges close to where we have positive matches. This allows us to more quickly converge on the result and stop the search early, although you may still miss some edges.
Overall, these methods are a speed up strategy that you may leverage over time to ensure fluidity, at the cost of graphical artifacts.
At this point however, our algorithm is not over! Indeed, we have only talked about the Extraction step, and will talk about the other ones in the next article of this series. Here is a quick overview in the meantime:
Visibility is the step where we find which lines are actually visible, and which ones aren't. This is the flipside of being able to detect invisible lines, and it's not trivial, as lines may get cut midway through by another object, so we need screen-space intersections.
Chaining comes after, and is the process of taking our individual edges and putting them together as part of a larger line. This helps us unlock more stylization options.
Finally, Stylization (and rendering) is the last step of our pipeline. This is where the fun is, but it is also more complex than it seems!
While extraction takes a lot of time, it is funnily enough the simplest step of the pipeline. You can expect the next article to be pretty beefy!
I hope you enjoyed reading this article! It took quite a while to make, and that's after I split it into three parts! We saw quite a lot, so let's quickly review what we learned:
There's a lack of resources online that really explain these kinds of topics in-depth, so this is an attempt to make the situation clearer. People are often blocked from making cool looking games because of a lack of technical and general knowledge of stylized rendering subjects, so if you're in that situation I hope this article finds you well!
Here's my general recommendations, which you may use as a starting point:
Of course, this is very simplified. The more complete recommendations are going to be in part 3, but this should already give you an idea.
We only looked at the first step today! Next time we will take a look at Stylization methods, where we will dissect what we can actually do with those lines we extracted, and
After that one, we will cash out all that knowledge in Part 3: How to do linework in practice! This is how we will finally take a clear look at how to implement our line detection pipelines, depending on engine and team, while avoiding common pitfalls and artifacts!
In the meantime, you could do well to register to the newsletter to not miss it when it releases! I also talk often about these subjects, so you can also join my Discord or follow me on Twitter!
Alright, see you in the next one!
Here are some additional parts if you want more!
Bibliography! Here's some of the papers / articles I cited here if you want to dive deeper into the subject.
So I've talked mostly about video game rendering, but not so much about offline (comics, movies, etc). To be fair, most techniques apply the same, except you don't care about runtime performance as much and it's easier to implement.
A big difference for these, is the fact that offline renderers tend to do raytracing, which doesn't really work with SSE, which is why they use the rays as a first step to reconstruct an image. For the other families, it tends to be similar to the real-time version.
Something that raytracing can do pretty well however is reflections and refractions, and this is supported by those line algorithms, but since it's pretty niche I won't expand on it further in this series.
Here's the list of nutshells that are in this article that you may have missed: